Kümnendmurdude ilmumine Babülonis. Esitlus - murrud Babylonis, Roomas, Egiptuses - kümnendmurdude avastamine
3.1.1. Murdude päritolu kohta.
Vajadus murdarvude järele tekkis inimese praktilise tegevuse tulemusena. Üksuse aktsiate leidmise vajadus ilmnes meie esivanemate seas pärast jahti saaki jagades. Murdarvude ilmumise teiseks oluliseks põhjuseks tuleks pidada suuruste mõõtmist valitud mõõtühiku abil.
Nii sündisid murded.
Murdarvu arengu ajaloos kohtame kolme tüüpi murde:
1) murrud või ühikmurrud, milles lugeja on üks, kuid nimetaja võib olla mis tahes täisarv;
2) süstemaatilised murrud, milles lugejateks võivad olla suvalised arvud, nimetajateks aga ainult teatud kindlat tüüpi arvud, näiteks kümne või kuuekümne astmed;
3) üldkuju murrud, milles lugejateks ja nimetajateks võivad olla suvalised arvud.
Nende kolme erinevat tüüpi murdude leiutamine valmistas inimkonnale erinevat raskusastet, nii et erinevatel ajastutel tekkisid erinevat tüüpi murded.
Inimese tutvus murdarvudega sai alguse väikese nimetajaga ühikmurdudest.
Mõisteid "pool", "kolmas", "veerand", "kaheksa" kasutavad sageli inimesed, kes pole kunagi õppinud murdarvude aritmeetikat. Need lihtmurrud mõtles iga rahvas oma arengu käigus iseseisvalt välja.
Esimene murdosa, millega inimesed kohtusid, oli pool. Kuigi kõigi järgmiste murdude nimed on seotud nende nimetajate nimedega (kolm - "kolmas", neli - "veerand" jne), ei kehti see poole kohta - selle nimel pole kõigis keeltes midagi. sõnaga "kaks". Järgmine murdosa oli kolmandik.
Seega on esimesed murrud, mida ajalugu meile tutvustab, vormi murrud - - nn ühikmurrud ehk alikvoodid (ladina keelest aliquot - "mitu").
Ühikumurrud on leitud vanimatest meieni jõudnud matemaatilistest tekstidest, mis on koostatud enam kui 5000 aastat tagasi - Vana-Egiptuse papüürused ja Babüloonia kiilkirjatahvlid.
Iidsetel aegadel saavutasid tavalised murded oma suurima arengu Indias. 4. sajandist eKr pärinevates käsikirjades ei leidu mitte ainult üksikmurde, vaid ka suvaliste lugejatega murde. 7. sajandi alguses teadsid ja sõnastasid indiaanlased harilike murdudega tehtavate reegleid. Lääne-Euroopas andis lõplikult väljakujunenud ja selge harilike murdude teooria 1585. aastal flaami insener Simon Stevin.
3.1.2. Murrud Vana-Egiptuses.
Vana-Egiptuses saavutas arhitektuur kõrge arengutaseme. Suurejooneliste püramiidide ja templite ehitamiseks, kujundite pikkuste, pindalade ja mahtude arvutamiseks oli vaja tunda aritmeetikat. Papüüruste dešifreeritud teabest said teadlased teada, et egiptlastel oli 4000 aastat tagasi kümnendarvu (kuid mitte positsiooniline) arvusüsteem, nad suutsid lahendada palju ehituse, kaubanduse ja sõjaliste küsimustega seotud probleeme. Egiptlased nimetasid sadu sajandeid murde "katkenenud arvudeks" ja esimene murd, mida nad kohtasid, oli 1/2. Sellele järgnesid 1/4, 1/8, 1/16, ..., siis 1/3, 1/6, ..., s.o. Lihtsamaid murde nimetatakse ühikmurdudeks. Nende lugeja on alati üks.
Egiptlased püüdsid kõiki murde kirjutada ühikmurdude (aktsiate) summadena. Näiteks kirjutamise asemel . Murd kirjutati aktsiate kujul: . Väga ebamugav on teha arvudega aritmeetilisi tehteid, lagundades need iga kord ühe murdude summaks. Kas egiptlaste kiindumusele alikvootide vastu on mingi seletus?
Selgitame seda näitega. Mõelge järgmisele probleemile: "Jagage 7 leiba 8 inimese vahel."
Siin on, kuidas see probleem lahendatakse Rhindi papüürusel, mis on Vana-Egiptuse matemaatiline tekst, mis on transkribeeritud umbes 1650 eKr. kirjatundja Ahmes.
Kuna . Seetõttu tuleks igale inimesele anda pool, veerand ja kaheksandik leiba. Nüüd on selge, et tuleb lõigata 4 pätsi pooleks, 2 pätsi 4 osaks ja ainult üks päts 8 osaks.
Ühikuta murdude laiendamiseks üksikuteks murdudeks olid valmis tabelid, mida Egiptuse kirjatundjad kasutasid vajalike arvutuste tegemiseks.
Võib näidata, et iga positiivset ratsionaalarvu saab esitada Egiptuse murdena. Seda tüüpi summat kasutasid matemaatikud murdude määratlusena Vana-Egiptuse ajast kuni keskajani. Kaasaegses matemaatikas kasutatakse Egiptuse murdude asemel liht- ja kümnendmurde, kuid arvuteoorias ja iidse matemaatika ajaloos uuritakse jätkuvalt Egiptuse murde.
3.1.3. Murrud Vana-Roomas.
Huvitav murdude süsteem oli Vana-Roomas. Roomlased kasutasid peamiselt ainult betoonfraktsioone, mis asendasid abstraktsed osad kasutatud mõõtude alajaotistega. See murdude süsteem põhines kaaluühiku jagamisel 12 osaks, mida nimetati perseiks. Nii tekkisid rooma kaksteistkümnendmurrud, s.o. murrud, mille nimetaja on alati 12. Ässa kaheteistkümnendikku nimetati untsiks. Ja viisi, aega ja muid koguseid võrreldi visuaalse asjaga - kaaluga. Näiteks võis roomlane öelda, et kõndis seitse untsi teed või luges viis untsi raamatut. Samas polnud see muidugi ka raja või raamatu kaalumises. See tähendas, et 7/12 teest sai läbi või 5/12 raamatust loetud. Ja murdude jaoks, mis saadi murdude taandamisel nimetajaga 12 või jagades kaheteistkümnendikud väiksemateks, olid spetsiaalsed nimetused.
Isegi praegu öeldakse mõnikord: "Ta uuris seda asja põhjalikult." See tähendab, et teemaga on lõpuni uuritud, et vähimatki ebaselgust pole jäänud. Ja kummaline sõna “skrupuluslikult” pärineb roomakeelsest nimest 1/288 assa - “scrupulus”. Kasutusel olid ka sellised nimed: "semis" - pool perset, "sextans" - selle kuues osa, "seven unts" - pool untsi, s.o. 1/24 perset jne. Kokku kasutati 18 erinevat murdnimetust. Murdudega töötamiseks oli vaja meeles pidada nende murdude liitmistabelit ja korrutustabelit. Seetõttu teadsid Rooma kaupmehed kindlalt, et trieeni (1/3 perse) ja sekstanide liitmisel saadakse semis ja kui deemon (2/3 perse) korrutatakse sescutsiooniga (2/3 untsi, s.o 1/8). perse), saadakse unts . Töö hõlbustamiseks koostati spetsiaalsed tabelid, millest osa on meieni jõudnud.
Isegi esimesel sajandil eKr ütles silmapaistev Rooma kõneleja ja kirjanik Cicero: "Ilma murdude tundmiseta ei saa kedagi tunnistada aritmeetikat tundvaks!".
Iseloomulik on järgmine väljavõte 1. sajandi eKr kuulsa Rooma poeedi Horatiuse teosest õpetaja ja õpilase vestlusest ühes tolle ajastu Rooma koolkonnas:
Õpetaja: Las Albini poeg ütleb, kui palju jääb alles, kui viiest untsist üks unts ära võetakse!
Õpilane: Üks kolmandik.
Õpetaja: Täpselt nii, sa tead hästi murde ja suudad oma vara päästa.
Nüüd on "perse" apteekri nael.
3.1.4. Babüloonia seksagesimaalsed murded.
Seksagesimaalse süsteemi päritolu on ebaselge. Võib-olla on see seotud kaksteistkümnendsüsteemiga (60 = 5 × 12, kus 5 on sõrmede arv käel). Samuti on olemas O. Neugebaueri hüpotees, et pärast Sumeri riigi vallutamist akadlaste poolt eksisteeris pikka aega samaaegselt kaks rahaühikut: seekel (sirp) ja mina ning nende suhteks kehtestati 1 miina = 60 seeklit. Hiljem sai see jaotus tuttavaks ja sellest sündis sobiv süsteem mis tahes numbrite kirjutamiseks.
20. sajandil Mesopotaamia lõunaosa iidsete linnade varemete vahel tehtud väljakaevamistel avastati suur hulk kiilkirjaga matemaatilisi tahvleid. Teadlased leidsid neid uurides, et 2000 aastat eKr. e. Matemaatika saavutas babüloonlaste seas kõrge arengutaseme.
Babüloonlaste kirjalik kuuekohaline numeratsioon ühendati kahest märgist: vertikaalsest kiilust ▼, mis tähistas ühte, ja kokkuleppemärgist ◄, mis tähistas kümmet.
Babüloonia kiilkirjatekstides kohtab esmalt positsioonilist arvusüsteemi. Vertikaalne kiil tähendas mitte ainult 1, vaid ka 60, 602, 603 jne. Alguses ei olnud babüloonlastel positsioonilises kuuekümnendsüsteemis nullimärki. Hiljem võeti numbrite üksteisest eraldamiseks kasutusele èè märk, mis asendas tänapäevase nulli.
Seksagesimaalarvusüsteemi tekkimine babüloonlaste seas on teadlaste hinnangul seotud sellega, et babüloonlaste raha- ja kaaluühikud jagunesid ajalooliste tingimuste tõttu 60 võrdseks osaks: 1 talent = 60 min; 1 mina = 60 seeklit. Kuuekümnendad olid babüloonlaste elus tavalised. Seetõttu kasutati seksagesimaalseid murde, millel on alati nimetaja 60 või selle astmed: 602 = 3600, 603 = 216 000 jne. Selles suhtes saab kuuekümnendmurdu võrrelda meie kümnendmurdudega. Babüloonia matemaatika mõjutas Kreeka matemaatikat. Kaasaegses teaduses on aja ja nurkade mõõtmisel säilinud jäljed Babüloonia seksagesimaalarvusüsteemist. Tänaseni on säilinud jaotus tund 60 minutiks, minut 60 sekundiks, ring 360 kraadiks, kraad 60 minutiks, minut 60 sekundiks. Babüloonlased andsid väärtusliku panuse astronoomia arengusse. Seksagesimaalseid murde kasutasid astronoomias kuni 17. sajandini kõigi rahvaste teadlased, nimetades neid astronoomilisteks murdudeks. Seevastu üldisi murde, mida me kasutame, nimetati tavalisteks murdudeks.
3.1.5. Nummerdamine ja murded Vana-Kreekas.
Kuni 6. sajandini eKr. e. Kreeka matemaatika polnud kuulus millegi silmapaistva poolest. Nagu ikka, meisterdati loendamist ja mõõtmist. Kreeka nummerdamine (arvude salvestamine), nagu hilisem rooma, oli aditiivne, see tähendab, et numbrite arvväärtused liideti. Selle esimene versioon (pööning ehk Herodes) sisaldas tähtmärke 1, 5, 10, 50, 100 ja 1000 jaoks. Vastavalt sellele oli paigutatud kivikestega loenduslaud (abacus). Muide, mõiste arvutamine (arvutamine) pärineb calculusest - kivike. Spetsiaalne auguline kivike, mis tähistas nulli.
Hiljem võeti pööningu nummerdamise asemel kasutusele tähestikuline nummerdamine - kreeka tähestiku 9 esimest tähte tähistasid numbreid 1 kuni 9, järgmised 9 tähte olid kümned, ülejäänud sajad. Et mitte numbreid ja tähti segi ajada, tõmmati numbrite kohale kriips. 1000-st suuremad numbrid kirjutati positsiooniliselt, märkides täiendavaid numbreid spetsiaalse joonega (all vasakul). Erimärgid võimaldasid kujutada numbreid, mis on suuremad kui 10 000.
VI sajandil eKr. e. Algab “Kreeka ime”: korraga ilmuvad kaks teaduslikku koolkonda - joonialased (Mileetose Thales, Anaximenes, Anaximander) ja Pythagoreanid. Varaste kreeka matemaatikute saavutustest teame peamiselt hilisemate autorite, peamiselt Eukleidese, Platoni ja Aristotelese kommentaaride põhjal.
Thales, jõukas kaupmees, õppis ilmselt oma kauplemisreisidel hästi Babüloonia matemaatikat ja astronoomiat. Ioonlased andsid esimesed geomeetriliste teoreemide tõestused.
Peamine roll iidse matemaatika loomisel kuulub siiski pütagoorlastele.
Vana-Kreekas eraldati aritmeetika – arvude üldiste omaduste uurimine – logistikast – arvutamise kunstist. Kreeklased uskusid, et murde saab kasutada ainult logistikas. Siin kohtame esmalt vormi m/n murdosa üldmõistet. Seega võib arvata, et esimest korda laienes looduslike arvude ala lisaratsionaalarvude alale Vana-Kreekas hiljemalt 5. sajandil eKr. e. Kreeklased kasutasid vabalt kõiki aritmeetilisi tehteid murdarvudega, kuid nad ei tunnistanud neid arvudena.
Kreeklased kasutasid koos üksikute "Egiptuse" murdudega tavalisi harilikke murde. Erinevate kirjete hulgas kasutati ka järgmist: nimetaja on peal, selle all murdosa lugeja.
1.4. Murrud Vana-Roomas.
Roomlased kasutasid peamiselt ainult betoonfraktsioone, mis asendasid abstraktsed osad kasutatud mõõtude alajaotistega. See murdude süsteem põhines kaaluühiku jagamisel 12 osaks, mida nimetati perseiks. Nii tekkisid rooma kaksteistkümnendmurrud, s.o. murrud, mille nimetaja on alati 12. Ässa kaheteistkümnendikku nimetati untsiks. 1/12 asemel ütlesid roomlased "üks unts", 5/12 - "viis untsi" jne. Kolm untsi nimetati veerandiks, neli untsi kolmandikuks, kuus untsi pooleks.
Ja viisi, aega ja muid koguseid võrreldi visuaalse asjaga - kaaluga. Näiteks võis roomlane öelda, et kõndis seitse untsi teed või luges viis untsi raamatut. Samas polnud see muidugi ka raja või raamatu kaalumises. See tähendas, et 7/12 teest sai läbi või 5/12 raamatust loetud. Ja murdude jaoks, mis saadi murdude taandamisel nimetajaga 12 või jagades kaheteistkümnendikud väiksemateks, olid spetsiaalsed nimetused. Kokku kasutati 18 erinevat murdnimetust. Näiteks olid kasutusel järgmised nimed:
"scrupulus" - 1/288 assa,
"poolperse" - poolperse,
"sextans" - selle kuues aktsia,
"seven untsi" - pool untsi, st. 1/24 perset jne.
Selliste murdudega töötamiseks oli vaja meeles pidada nende murdude liitmistabelit ja korrutustabelit. Seetõttu teadsid Rooma kaupmehed kindlalt, et trieeni (1/3 perse) ja sekstanide liitmisel saadakse semis ja kui deemon (2/3 perse) korrutatakse sescutsiooniga (2/3 untsi, s.o 1/8). perse), saadakse unts . Töö hõlbustamiseks koostati spetsiaalsed tabelid, millest osa on meieni jõudnud.
Untsi tähistati mõttekriipsuga – pool assa (6 untsi) – tähega S (esimene ladinakeelses sõnas Semis on pool). Need kaks märki olid mõeldud mis tahes kaheteistkümnendmurru kirjutamiseks, millest igaühel oli oma nimi. Näiteks 7 \ 12 kirjutati nii: S-.
Isegi esimesel sajandil eKr ütles silmapaistev Rooma kõneleja ja kirjanik Cicero: "Ilma murdude tundmiseta ei saa kedagi tunnistada aritmeetikat tundvaks!".
Iseloomulik on järgmine väljavõte 1. sajandi eKr kuulsa Rooma poeedi Horatiuse teosest, mis räägib õpetaja ja õpilase vestlusest ühes tolle ajastu Rooma koolidest:
Õpetaja: Las Albini poeg ütleb, kui palju jääb alles, kui viiest untsist üks unts ära võetakse!
Õpilane: Üks kolmandik.
Õpetaja: Täpselt nii, sa tead hästi murde ja suudad oma vara päästa.
1.5. Murrud Vana-Kreekas.
Vana-Kreekas eraldati aritmeetika – arvude üldiste omaduste uurimine – logistikast – arvutamise kunstist. Kreeklased uskusid, et murde saab kasutada ainult logistikas. Kreeklased kasutasid vabalt kõiki aritmeetilisi tehteid murdarvudega, kuid nad ei tunnistanud neid arvudena. Kreeka matemaatikateemalistes kirjutistes polnud murde. Kreeka teadlased uskusid, et matemaatika peaks tegelema ainult täisarvudega. Nad varustasid murdosaga kaupmehi, käsitöölisi, aga ka astronome, geodeete, mehaanikuid ja teisi "mustaid inimesi". "Kui soovite ühikut jagada, naeruvääristavad matemaatikud teid ega luba teil seda teha," kirjutas Ateena Akadeemia asutaja Platon.
Kuid mitte kõik Vana-Kreeka matemaatikud ei nõustunud Platoniga. Nii et traktaadis "Ringi mõõtmise kohta" kasutab Archimedes murde. Aleksandria heron võis vabalt ka murdosasid käsitleda. Tema, nagu egiptlased, jagab murdosa põhimurdude summaks. 12\13 asemel kirjutab ta 1\2 + 1\3 + 1\13 + 1\78, 5\12 asemel 1\3 + 1\12 jne. Isegi Pythagoras, kes suhtus naturaalarvudesse püha aukartusega, ühendas muusikalise skaala teooriat luues peamised muusikalised intervallid murdosadega. Tõsi, Pythagoras ja tema õpilased ei kasutanud murdosa mõistet. Nad lubasid endal rääkida ainult täisarvude suhetest.
Kuna kreeklased tegelesid murdudega vaid juhuslikult, kasutasid nad erinevaid tähistusi. Heron ja Diophantus kirjutasid murde tähestikulises vormis, nimetaja all oli lugeja. Mõnede murdude jaoks kasutati eraldi tähistusi, näiteks 1 \ 2 - L ′′, kuid üldiselt ei võimaldanud nende tähestikuline nummerdamine murdude tähistamist.
Ühikumurdude puhul kasutati spetsiaalset tähistust: murru nimetajale kaasnes kriips paremal, lugejat ei kirjutatud. Näiteks tähestikulises süsteemis tähendas see 32 ja "- murd 1 \ 32. Tavaliste murdude kohta on selliseid kirjeid, kus joonega lugeja ja kahe joonega kaks korda võetav nimetaja on kirjutatud kõrvuti ühele reale. Näiteks kirjutas Aleksandria Heron murdosa 3 \neli järgmiselt: 
.
Murdarvude kreeka tähistuse puudused tulenevad asjaolust, et kreeklased mõistsid sõna "arv" ühikute kogumina, seetõttu mõistsid kreeklased seda, mida me praegu käsitleme ühtse ratsionaalarvuna - murruna - suhtena. kahest täisarvust. See seletab, miks harilikud murrud olid kreeka aritmeetikas haruldased. Eelistati kas ühe lugejaga murde või seksagesimaalseid murde. Valdkond, kus praktilistel arvutustel oli kõige suurem vajadus täpsete murdude järele, oli astronoomia ja siin oli Babüloonia traditsioon nii tugev, et seda kasutasid kõik rahvad, sealhulgas Kreeka.
1.6. Murrud Venemaal
Esimene vene matemaatik, meile nimepidi tuntud Novgorodi kloostri munk Kirik, tegeles kronoloogia ja kalendri küsimustega. Tema käsitsi kirjutatud raamatus “Tema õpetus inimeste kõigi aastate numbreid tundmaõppimiseks” (1136), s.o. “Juhend, kuidas inimene saab teada aastate arvu” rakendab tunni jagamist viiendikuteks, kahekümneviiendikuteks jne. murdosad, mida ta nimetas "murrutundideks" või "tundideks". Ta jõuab seitsmenda murdtunnini, millest päevas või öös on 937 500, ja ta ütleb, et seitsmendast murdtunnist ei saada midagi.
Esimestes matemaatikaõpikutes (7. sajand) nimetati murde murdudeks, hiljem "katkearvudeks". Vene keeles ilmus sõna murd 8. sajandil, see tuleb verbist "purustama" - murdma, tükkideks murdma. Numbri kirjutamisel kasutati horisontaalset joont.
Vanades juhendites on Venemaal järgmised murdude nimed:
1/2 - pool, pool
1/3 - kolmas
1/4 - neli
1/6 - pool kolmandikku
1/8 - poolteist tundi
1/12 - pool kolmandikku
1/16 - pool 16
1/24 - pool-pool kolmandik (väike kolmandik)
1/32 - pool ja pool ja pool (väike veerand)
1/5 - viis
1/7 - nädal
1/10 - kümnis.
Venemaal kasutati veerand ja väiksem maamõõt -
pool neljandikku, mida kutsuti kaheksajalaks. Need olid konkreetsed murrud, ühikud Maa pindala mõõtmiseks, kuid kaheksajalg ei saanud mõõta aega ega kiirust jne. Palju hiljem hakkas kaheksajalg tähendama abstraktset murdosa 1/8, mis võib väljendada mis tahes väärtus.
Murdude kasutamisest Venemaal 17. sajandil saab lugeda V. Bellustini raamatust “Kuidas järk-järgult jõuti tõelise aritmeetikani” järgmist: “17. sajandi käsikirjas. "Kõigi aktsiate arvuline artikkel, dekreet "algab vahetult murdude kirjaliku tähistamisega ning lugeja ja nimetaja märkimisega. Murdude hääldamisel on huvitavad järgmised tunnused: neljandat osa nimetati veerandiks, samas kui nimetajaga 5–11 osakaalu väljendati sõnadega lõpuga “ina”, seega 1/7 on nädal, 1/5 on viis, 1/10 on kümnis; aktsiad, mille nimetaja oli suurem kui 10, hääldati sõnadega "varsad", näiteks 5/13 - viis kolmeteistkümnendat partiid. Murdude numeratsioon laenati otse lääne allikatest ... Lugejat nimetati ülemiseks numbriks, nimetajat alumiseks.
Alates 16. sajandist on plankkonto Venemaal olnud väga populaarne – arvutused Vene arvete prototüübiks olnud instrumendi abil. See võimaldas kiiresti ja lihtsalt sooritada keerulisi aritmeetilisi tehteid. Plangukonto oli väga levinud kaupmeeste, Moskva ordude töötajate, "mõõtjate" - maamõõtjate, kloostri kojameeste jne seas.
Algsel kujul oli tahvlite arv spetsiaalselt kohandatud arenenud aritmeetika vajadustele. See on maksustamissüsteem Venemaal 15.–17. sajandil, kus koos täisarvude liitmise, lahutamise, korrutamise ja jagamisega tuli teha samad toimingud murdosadega, kuna maksustamise tingimuslik ühik - ader, jagati osadeks.
Plangukonto koosnes kahest kokkupandavast kastist. Iga kast oli jagatud kaheks (hiljem ainult põhja); teine kast oli vajalik rahakonto iseärasuste tõttu. Kasti sees olid kondid nööritud venitatud nööride või traadi külge. Kümnendarvude süsteemi kohaselt oli täisarvude ridadel 9 või 10 luud; toimingud murdosadega tehti mittetäielikel ridadel: kolmest luust koosnev rida moodustas kolm kolmandikku, neljast luust koosnev rida - neli neljandikku (cheti). Allpool olid read, milles oli üks luu: iga luu esindas poolt fraktsioonist, mille all see asus (näiteks kolme luu rea all asuv luu oli pool kolmandikust, selle all olev luu pool ühest poolest kolmandikust jne). Kahe identse “sarnase” murru liitmine annab murdosa lähimast kõrgemast kategooriast, näiteks 1/12+1/12=1/6 jne. Kontodel vastab kahe sellise fraktsiooni lisamine üleminekule lähima kõrgemale näpule.
Murrud summeeriti ilma taandamata ühise nimetajani, näiteks "veerand ja pool ja pool" (1/4 + 1/6 + 1/16). Mõnikord tehti murdudega tehteid nagu täisarvudega, võrdsustades kogu (ader) teatud rahasummaga. Näiteks kui sokha = 48 rahaühikut, on ülaltoodud murd 12 + 8 + 3 = 23 rahaühikut.
Sosh-aritmeetikas tuli tegeleda väiksemate murdudega. Mõned käsikirjad pakuvad jooniseid ja kirjeldusi "arvutuskastide" kohta, mis sarnanevad äsja vaadeldud, kuid millel on palju ühe luuga ridu, nii et nendele saab kõrvale jätta kuni 1/128 ja 1/96 fraktsioonid. Kahtlemata tehti ka vastavaid seadmeid. Kalkulaatorite mugavuse huvides anti palju "Väikeste luude koodeksi" reegleid, st. sosh kontol kasutatavate fraktsioonide lisamine, nagu: kolmveerand adra ja pool adra ja poolteist adra jne. kuni pool-pool-pool-pool ader on ader ilma pool-pool-pool-poolveerandita, s.o. 3/4+1/8+1/16+1/32 +1/64 + 1/128 = 1 - 1/128 jne.
Kuid murdudest võeti arvesse ainult 1/2 ja 1/3, samuti neid, mis saadi neist järjestikuse 2-ga jagamise teel. Teiste seeriate murdosadega tehte puhul ei kohandatud "tahvlite arvu". Nendega opereerides tuli viidata spetsiaalsetele tabelitele, milles olid toodud erinevate murdude kombinatsioonide tulemused.
AT 1703 Ilmub esimene vene trükitud matemaatikaõpik "Aritmeetika". Autor Magnitski Leonty Filippovitš. Selle raamatu 2. osas „Katkestatud joonte arvudest või osadest” kirjeldatakse murdude õpetust üksikasjalikult.
Magnitski puhul on sellel peaaegu kaasaegne iseloom. Magnitski peatub aktsiate arvutamisel põhjalikumalt kui tänapäevased õpikud. Magnitski peab murde nimelisteks arvudeks (mitte ainult 1/2, vaid 1/2 rubla, pood jne) ja ta uurib ülesannete lahendamise protsessis toiminguid murdosadega. Et on katkine arv, vastab Magnitski: “Katkine arv pole midagi muud, ainult numbriga deklareeritud asja osa ehk kirjutatakse pool rubla, aga kirjutatakse rublas ehk rublas või rubla ehk kaks viiendikku ja igasugu asju kas osa deklareeritud arvuna ehk siis katkine arv. Magnitski annab kõigi õigete murdude nimed nimetajatega 2 kuni 10. Näiteks murded, mille nimetaja on 6: üks kuusteist, kaks kuusteist, kolm kuusteist, neli kuusteist, viis kuusteist.
Magnitsky kasutab nimelugejat, nimetajat, arvestab valede murdudega, segaarvudega, lisaks kõikidele toimingutele eristab ta valest murdest terve osa.
Murdude õpetus on alati jäänud aritmeetika kõige keerulisemaks haruks, kuid samal ajal mõistsid inimesed igal varasemal ajastul murdude uurimise tähtsust ning värsi- ja proosaõpetajad püüdsid oma õpilasi rõõmustada. L. Magnitski kirjutas:
Aga aritmeetikat pole
Ijo terves süüdistatavas,
Ja nendes aktsiates pole midagi,
Saate vastata.
söö sinust rõõmusta,
Oskab osade kaupa.
1.7. Murrud iidses Hiinas
Hiinas kehtestati peaaegu kõik aritmeetilised tehted harilike murdudega juba 2. sajandil eKr. eKr e.; neid kirjeldatakse Vana-Hiina matemaatikateadmiste fundamentaalses korpuses – "Matemaatika üheksas raamatus", mille viimane väljaanne kuulub Zhang Cangile. Eukleidese algoritmiga sarnase reegli (lugeja ja nimetaja suurim ühine jagaja) alusel arvutades vähendasid Hiina matemaatikud murde. Murdude korrutamine esitati ristkülikukujulise maatüki pindala leidmisena, mille pikkus ja laius on väljendatud murdarvudes. Jagamist kaaluti jagamise ideed kasutades, samas kui Hiina matemaatikud ei tundnud piinlikkust, et jagamises osalejate arv võis olla murdosa, näiteks 3⅓ inimest.
Algselt kasutasid hiinlased lihtsamaid murde, mis said nime bani hieroglüüfi abil:
vannid ("pool") -1 \ 2;
shao keeld ("väike pool") -1\3;
tai keeld ("suur pool") -2 \ 3.
Järgmine samm oli murdude üldise idee väljatöötamine ja nendega töötamise reeglite kujundamine. Kui Vana-Egiptuses kasutati ainult alikvootseid fraktsioone, siis Hiinas peeti neid fraktsioonideks, mitte aga ainsaks võimalikuks. Hiina matemaatika on segaarvudega tegelenud iidsetest aegadest peale. Varaseim matemaatiline tekst, Zhou Bi Suan Jing (Zhou Gnomoni arvutamise kaanon / Gnomoni matemaatiline traktaat), sisaldab arvutusi, milles arvud, näiteks 247933/1460, tõstetakse astmeni.
Teoses "Ju zhang suan shu" ("Üheksa jaotise loendamise reeglid") käsitletakse murdosa terviku osana, mis on väljendatud selle murdude n-ndas arvus - fen - m (n
"Ju Zhang Suan Shu" esimeses osas, mis on üldiselt pühendatud väljade mõõtmisele, murdude vähendamise, liitmise, lahutamise, jagamise ja korrutamise reeglid, samuti nende võrdlemine ja "võrdsustamine", s.o. selline kolme murru võrdlus, milles on vaja leida nende aritmeetiline keskmine (lihtsamat reeglit kahe arvu aritmeetilise keskmise arvutamiseks raamatus ei ole toodud).
Näiteks selles essees olevate murdude summa saamiseks pakutakse järgmist juhist: „Korrutage (hu cheng) lugejad vaheldumisi nimetajatega. Liida kokku – see on dividend (shi). Korrutage nimetajad - see on jagaja (fa). Kombineerige dividend jagajaga üheks (ja). Kui on jääk, siis seosta see jagajaga. See käsk tähendab, et kui liita mitu murru, siis tuleb iga murru lugeja korrutada kõigi teiste murdude nimetajatega. Dividendi (sellise korrutamise tulemuste summana) “ühendamisel” jagajaga (kõigi nimetajate korrutis) saadakse murd, mida tuleks vajadusel vähendada ja millest kogu osa jagamisega eraldada. , siis on "ülejääk" lugeja ja vähendatud jagaja on nimetaja. Murdude hulga summa on sellise jagamise tulemus, mis koosneb täisarvust pluss murdosast. Käsk "nimetajate korrutamine" tähendab tegelikult murdude viimist suurima ühisnimetajani.
Murru vähendamise reegel Jiu Zhang Xuan Shu sisaldab algoritmi lugeja ja nimetaja suurima ühisjagaja leidmiseks, mis on sama, mis nn Eukleidese algoritm kahe arvu suurima ühisjagaja leidmiseks. Aga kui viimane, nagu teada, on "Põhimõttes" antud geomeetrilises sõnastuses, siis hiina algoritm esitatakse puhtalt aritmeetiliselt. Hiina algoritm suurima ühise jagaja leidmiseks, mida nimetatakse den shu-ks ("sama arv"), on üles ehitatud väiksema arvu järjestikuse lahutamisena suuremast. See on den shu arv ja seda on vaja vähendada. Näiteks tehakse ettepanek vähendada murdosa 49\91. Viime läbi järjestikuse lahutamise: 91 - 49 \u003d 42; 49 - 42 = 7; 42 - 7 - 7 - 7 - 7 - 7 - 7 \u003d 0. Deng shu \u003d 7. Vähendame murdosa selle arvu võrra. Saame: 7 \ 13.
"Ju Zhang Xuan Shu" murdude jaotus erineb tänapäeval aktsepteeritavast. Reegel "ching fen" ("jagamise järjekord") ütleb, et enne murdude jagamist tuleks need taandada ühiseks nimetajaks. Seega on murdude jagamise protseduuril tarbetu samm: a/b: c/d = ad/bd: cb/bd = ad/cb. Alles 5. sajandil Zhang Qiu-jian sai teoses “Zhang Qiu-jian suan jing” (“Zhang Qiu-jiani loendamiskaanon”) sellest lahti, jagades murde tavapärase reegli järgi: a/b: c/d = ad/cb. .
Võib-olla oli Hiina matemaatikute pikaajaline pühendumine keerukale murdude jagamise algoritmile tingitud soovist säilitada selle universaalsus ja loenduslaua kasutamine. Tegelikult seisneb see murdude jagamise taandamises täisarvude jagamiseks. See algoritm kehtib, kui täisarv jagub segaarvuga. Näiteks jagades 2922 arvuga 182 5/8, korrutati mõlemad arvud kõigepealt 8-ga, mis võimaldas täisarvu edasist jagamist: 23376:1461= 16
1.8. Murrud teistes antiikseisundites ja keskajal.
Hariliku murdosa kontseptsiooni edasiarendamine saavutati Indias. Selle riigi matemaatikud suutsid kiiresti liikuda ühikmurdudelt üldkuju murdude juurde. Esimest korda leidub selliseid murde Apastamba (VII-V sajand eKr) "Nöörireeglites", mis sisaldavad geomeetrilisi konstruktsioone ja mõningate arvutuste tulemusi. Indias kasutati kirjutamissüsteemi - võib-olla hiina ja võib-olla hiliskreeka päritolu -, kus murdu lugeja kirjutati nimetaja kohale - nagu meilgi, kuid ilma murdejooneta, kuid kogu murd paigutati ristkülikukujuline raam. Mõnikord kasutati ka "kolmekorruselist" väljendit, kus ühes kaadris oli kolm numbrit; olenevalt kontekstist võib see tähendada vale murdosa (a + b/c) või täisarvu a jagamist murdosaga b/c.
Näiteks murdosa 
salvestatud kui
India teadlase Bramagupta (VIII sajand) kehtestatud murdosadega toimingute reeglid ei erinenud palju tänapäevastest. Nagu Hiinas, nii ka Indias korrutati ühisnimetajaks taandamiseks pikka aega kõikide mõistete nimetajaid, kuid alates 9. sajandist. kasutas vähimat ühiskorda.
Keskaegsed araablased kasutasid murdude kirjutamiseks kolme süsteemi. Esiteks, india moodi, nimetaja kirjutamine lugeja alla; murdjoon tekkis 12. sajandi lõpus - 13. sajandi alguses. Teiseks kasutasid ametnikud, maamõõtjad, kaupmehed alikvoodi murdude arvutamist sarnaselt egiptuse omaga, samas kui murde, mille nimetaja ei ületanud 10 (araabia keeles on eriterminid ainult selliste murdude kohta); sageli kasutati ligikaudseid väärtusi; Araabia teadlased töötasid selle arvutuse parandamiseks. Kolmandaks pärisid araabia teadlased Babüloonia-Kreeka kuuekümnendsüsteemi, milles sarnaselt kreeklastega kasutasid nad tähestikulist tähistust, laiendades seda tervetele osadele.
India murdude tähistus ja nendega töötamise reeglid assimileeriti 9. sajandil. moslemimaades tänu Khorezmi Muhamedile (al-Khwarizmi). Islamimaade kaubanduspraktikas olid laialdaselt kasutusel üksikmurrud, teaduses kasutati kuueaastaseid murde ja palju vähemal määral tavalisi murde. Al-Karaji (X-XI sajand), al-Khassar (XII sajand), al-Kalasadi (XV sajand) ja teised teadlased esitasid oma töödes reeglid tavaliste murdude esitamiseks ühikmurdude summade ja korrutistena. Teabe murdude kohta edastas Lääne-Euroopasse Itaalia kaupmees ja teadlane Leonardo Fibonacci Pisast (XIII sajand). Ta võttis kasutusele sõna murd, hakkas kasutama murru tunnust (1202), andis valemid murdude süstemaatiliseks jaotamiseks põhilisteks. Nimed lugeja ja nimetaja võttis 13. sajandil kasutusele kreeka munk, teadlane ja matemaatik Maxim Planud. Meetodi murdude ühiseks nimetajaks taandamiseks pakkus 1556. aastal välja N. Tartaglia. Kaasaegne tavaliste murdude liitmise skeem on leitud 1629. aastast. A. Girardi juures.
II. Tavaliste murdude kasutamine
2.1 Alikvoodifraktsioonid
Alikvootfraktsioonide kasutamisega seotud probleemid moodustavad ulatusliku mittestandardsete probleemide klassi, sealhulgas need, mis on pärit iidsetest aegadest. Alikvootfraktsioone kasutatakse siis, kui midagi on vaja jagada mitmeks osaks, mille jaoks on vaja kõige vähem samme. Vormi 2/n ja 2/(2n + 1) murdude lagunemine kaheks alikvoodiks on süstematiseeritud valemite kujul
Lagundamine kolmeks, neljaks, viieks jne. alikvoodifraktsioone saab valmistada, jagades ühe terminitest kaheks, järgmise fraktsiooni veel kaheks alikvoodifraktsiooniks jne.
Mis tahes arvu esitamiseks alikvoodi murdude summana peate mõnikord üles näitama erakordset leidlikkust. Oletame, et arvu 2/43 väljendatakse järgmiselt: 2/43=1/42+1/86+1/129+1/301. Väga ebamugav on teha arvudega aritmeetilisi tehteid, lagundades need ühe murdude summaks. Seetõttu tekkis alikvoodimurdude kui väiksemate alikvoodimurdude summana alikvoodimurdude paisutamise ülesannete lahendamise käigus mõte murdude laiendamine valemi kujul süstematiseerida. See valem kehtib, kui on vaja alikvoodifraktsiooni laiendada kaheks alikvoodifraktsiooniks.
Valem näeb välja selline:
1/n=1/(n+1) + 1/n (n+1)
Näited fraktsioonide laiendamise kohta:
1/3=1/(3+1)+1/3 (3+1)=1/4 +1/12;
1/5=1/(5+1)+1/5 (5+1)=1/6 +1/30;
1/8=1/(8+1)+1/8 (8+1)=1/9+ 1/72.
Seda valemit saab teisendada ja saada järgmise kasuliku võrdsuse: 1/n (n+1)=1/n -1/(n+1)
Näiteks 1/6=1/(2 3)=1/2 -1/3
See tähendab, et alikvoodi murdosa saab esitada kahe alikvoodi murru erinevuse või kahe alikvoodi murru erinevusena, mille nimetajad on järjestikused arvud, mis on võrdsed nende korrutisega.
Näide. Esitage arv 1 erinevate alikvoodi murdude summadena
a) kolm liiget 1=1/2+1/2=1/2+(1/3+1/6)=1/2+1/3+1/6
b) neli terminit
1=1/2+1/2=1/2+(1/3+1/6)=1/2+1/3+1/6=1/2+1/3+(1/7+1/42)= 1/2+1/3+1/7+1/42
c) viis terminit
1=1/2+1/2=1/2+(1/3+1/6)=1/2+1/3+1/6=1/2+1/3+(1/7+1/42)=1/2+1/3+1/7+1/42=1/2+(1/4+ +1/12) +1/7+1/42=1/2+1/4+1/12 +1/7+1/42
2.2 Väikeste aktsiate asemel suured
Masinaehitustehastes on väga põnev elukutse, seda kutsutakse kirjutajaks. Kirjutaja märgib toorikule jooned, mida mööda töödeldavat detaili tuleb töödelda, et anda sellele vajalik kuju.
Kirjutaja peab lahendama huvitavaid ja kohati keerulisi geomeetrilisi ülesandeid, sooritama aritmeetilisi arvutusi jne.
"Oli vaja kuidagi jaotada 7 ühesugust ristkülikukujulist plaati võrdsetes osades 12 osa vahel. Nad tõid need 7 plaati markeri juurde ja palusid tal võimalusel plaadid märgistada nii, et ühtegi neist ei peaks väga väikesteks osadeks purustama. Nii et kõige lihtsam lahendus on iga kirje 12 võrdseks osaks lõikamine ei olnud hea, kuna tulemuseks oli palju väikeseid osi.
Kas neid plaate on võimalik suuremateks osadeks jagada? Skaleerija mõtles, tegi murdarvudega aritmeetilisi arvutusi ja leidis siiski kõige ökonoomsema viisi nende plaatide jagamiseks.
Seejärel purustas ta hõlpsalt 5 plaati, et jagada need võrdsetes osades kuue osa vahel, 13 plaati 12 osa jaoks, 13 plaati 36 osa jaoks, 26 plaati 21 jaoks jne.
Selgub, et marker kujutas murdosa 7\12 ühikuliste murdude 1\3 + 1\4 summana. Seega, kui 7 antud plaadist lõigatakse 4 kolmeks võrdseks osaks, saame 12 kolmandikku, see tähendab ühe kolmandiku iga osa kohta. Ülejäänud 3 plaati lõikasime 4 võrdseks osaks, saame 12 veerandit, see tähendab iga osa jaoks veerandi. Samamoodi kasutades murdude esitusi ühikuliste murdude summana 5\6=1\2+1\3; 13\121\3+3\4; 13\36=1\4+1\9.
2.3 Vaheseinad rasketes oludes
On tuntud idamaine tähendamissõna, et isa jättis oma poegadele 17 kaamelit ja käskis neil omavahel jagada: vanem pool, keskmine - kolmandik, noorem - üheksandik. Kuid 17 ei jagu 2, 3 ega 9-ga. Pojad pöördusid targa poole. Tark tundis murdosasid ja oskas selles keerulises olukorras aidata.
Ta läks triki peale. Tark lisas oma kaameli mõneks ajaks karja, siis oli neid 18. Jagades selle arvu, nagu testamendis kirjas, võttis tark oma kaameli tagasi. Saladus seisneb selles, et osad, millesse tahtmise järgi pidid pojad karja jagama, ei anna kokku 1. Tõepoolest, 1\2 + 1\3 + 1\9 = 17\18.
Selliseid ülesandeid on palju. Näiteks ülesanne venekeelsest õpikust 4 sõbra kohta, kes leidsid rahakoti 8 kreeditarvega: üks ühe, kolm, viis rubla ja ülejäänud kümme rubla. Vastastikusel kokkuleppel sooviti kolmandat osa, teist veerandit, kolmandat-viiendat, neljandat-kuuendat. Omal jõul nad aga hakkama ei saanud: üks mööduja aitas, pärast oma rubla lisamist. Selle raskuse lahendamiseks lisas mööduja ühikumurrud 1\3 + 1\4 + 1\5 + 1\6 = 57\60, rahuldades sõprade taotlused ja teenides endale 2 rubla.
III.Meelelahutuslikud fraktsioonid
3.1 Doomino
Doomino on lauamäng, mida mängitakse kõikjal maailmas. Doominomäng koosneb enamasti 28 ristkülikukujulisest kivist-täringust. Doomino on ristkülikukujuline plaat, mille esikülg on joonega jagatud kaheks ruudukujuliseks osaks. Iga osa sisaldab nullist kuue punktini. Kui eemaldada täringud, mis ei sisalda punkte vähemalt ühel poolel (blankhe), siis võib ülejäänud täringut lugeda murdudena. Luud, mille mõlemad pooled sisaldavad sama arvu punkte (kahekordseid), on ühega võrdsed valemurrud. Kui neid luid rohkem eemaldada, jääb alles 15 luud. Neid saab paigutada erinevalt ja saada huvitavaid tulemusi.
1. Paigutus 3 rida, millest igaühe murdude summa on 2.
;
;
2. Paigaldage kõik 15 paani kolmes reas, millest igaühes on 5 paani, kasutades mõnda doominoplaati sobimatute murdudena, näiteks 4/3, 6/1, 3/2 jne, nii et iga murdude summa rida oli võrdne 10-ga.
1\3+6\1+3\4+5\3+5\4=10
2\1+5\1+2\6+6\3+4\6=10
4\1+2\3+4\2+5\2+5\6=10
3. Paigutus murdude ridadesse, mille summaks saab täisarv (kuid erinevates ridades erinev).
3.2 Juba ammusest ajast.
"Ta uuris seda küsimust põhjalikult." See tähendab, et teemaga on lõpuni uuritud, et vähimatki ebaselgust pole jäänud. Ja kummaline sõna “skrupuluslikult” pärineb roomakeelsest nimest 1/288 assa - “scrupulus”.
"Astuge murdosadesse." See väljend tähendab raskesse olukorda sattumist.
"Ass" - massiühik farmakoloogias (apteekri nael).
"Unts" - massiühik inglise mõõdusüsteemis, massiühik farmakoloogias ja keemias.
IV. Järeldus.
Murdude õpetust peeti matemaatika kõige raskemaks osaks kõigil aegadel ja kõigi rahvaste seas. Neid, kes murdsid tundsid, peeti väga lugu. Vana 15. sajandi slaavi käsikirja autor. kirjutab: "Ei ole üllatav, et ... tervikuna, aga kiiduväärt on see, et aktsiates ...".
Järeldasin, et harilike murdude ajalugu on käänuline tee, millel on palju takistusi ja raskusi. Essee kallal töötades sain teada palju uut ja huvitavat. Lugesin palju raamatuid ja entsüklopeediate rubriike. Tutvusin esimeste murdudega, millega inimesed opereerisid, alikvootmurru mõistega, õppisin enda jaoks uusi nimetusi teadlastele, kes aitasid kaasa murdude õpetuse väljatöötamisele. Ta püüdis ise lahendada olümpiaadi- ja meelelahutusülesandeid, valis iseseisvalt näiteid harilike murdude alikvootmurrudeks lagundamisest, analüüsis tekstides toodud näidete ja ülesannete lahendusi. Vastus küsimusele, mille esitasin endale enne essee kallal töötamist: tavalised murrud on vajalikud, need on olulised. Ettekande koostamine oli huvitav, pidin abi saamiseks pöörduma õpetaja ja klassikaaslaste poole. Samuti puutusin tippimisel esimest korda kokku vajadusega trükkida murde ja murdosa avaldisi. Esitlesin oma kokkuvõtet koolikonverentsil. Ta esines ka klassikaaslaste ees. Nad kuulasid väga tähelepanelikult ja minu arvates olid nad huvitatud.
Arvan, et ülesanded, mille seadsin enne abstraktse kallal töötamist, on minu poolt täidetud.
Kirjandus.
1. Borodin A.I. Aritmeetika ajaloost. Juhtiv kirjastus "Vishcha kool" -K., 1986
2. Glazer G. I. Matemaatika ajalugu koolis: IV-VI kl. Juhend õpetajatele. – M.: Valgustus, 1981.
3. Ignatiev E.I. Leidlikkuse vallas. Kirjastuse "Nauka" füüsikalise ja matemaatilise kirjanduse põhiväljaanne, M., 1978.
4. Kordemskoy G.A. Matemaatiline leidlikkus. – 10. väljaanne, läbivaadatud. Ja täiendav - M .: Yunisam, MDS, 1994.
5. Stroyk D.Ya. Lühiülevaade matemaatika ajaloost. Moskva: Nauka, 1990.
6. Entsüklopeedia lastele. Köide 11. Matemaatika. Moskva, "Avanta +", 1998.
7. /wiki Materjal Wikipediast – vabast entsüklopeediast.
Lisa 1.
Looduslik skaala
Kõik teavad, et Pythagoras oli teadlane ja eriti kuulsa teoreemi autor. Ja see, et ta oli ka geniaalne muusik, pole laialt teada. Nende annete kombinatsioon võimaldas tal olla esimene, kes aimab loodusliku skaala olemasolu. Pidime seda veel tõestama. Pythagoras ehitas oma katsete jaoks poolinstrumendi-poolseadme – "monokordi". See oli piklik karp, mille peale oli tõmmatud nöör. Nööri alla, karbi ülemisele kaanele, joonistas Pythagoras skaala, et oleks lihtsam nööri visuaalselt osadeks jagada. Pythagoras tegi palju katseid monokordiga ja lõpuks kirjeldas ta matemaatiliselt kõlava stringi käitumist. Pythagorase looming moodustas aluse teadusele, mida praegu nimetame muusikaakustikaks. Selgub, et seitse heli oktavis on muusika jaoks sama loomulikud kui kümme sõrme aritmeetikas. Juba esimese poogna vibunöör, mis pärast lasku võngus, andis valmis selle muusikalise helistiku, mida kasutame siiani peaaegu muutumatuna.
Füüsika seisukohalt on vibunöör ja nöör üks ja seesama. Jah, ja mees tegi nööri, pöörates tähelepanu vibunööri omadustele. Kõlav keel ei võngu mitte ainult tervikuna, vaid samaaegselt pooleks, tertsiks, veerandiks jne. Lähenegem nüüd sellele nähtusele aritmeetilisest küljest. Pooled vibreerivad kaks korda sagedamini kui terve string, kolmandikud - kolm korda, veerandid - neli korda. Ühesõnaga, mitu korda on nööri vibreeriv osa väiksem, sama palju kordi suurem on selle vibratsioonide sagedus. Oletame, et kogu string vibreerib sagedusega 24 hertsi. Arvutades aktsiate kõikumised kuni kuueteistkümnendikuni, saame tabelis näidatud arvude jada. Seda sageduste jada nimetatakse loomulikuks, s.t. loomulik, heli.
2. lisa
Muistsed ülesanded tavaliste murdude kasutamisel.
Erinevate maade iidsetes käsikirjades ja iidsetes aritmeetikaõpikutes on palju huvitavaid ülesandeid murdude kohta. Kõigi nende probleemide lahendamine nõuab märkimisväärset leidlikkust, leidlikkust ja arutlusvõimet.
1. Karjane tuleb 70 pulliga. Temalt küsitakse:
Kui palju sa oma arvukast karjast välja tood?
Karjane vastab:
Toon kaks kolmandikku kolmandikust veistest. Loendage, mitu pulli on karjas?
Ahmese papüürus (Egiptus, umbes 2000 eKr).
2. Keegi võttis riigikassast 1/13. Sellest, mis üle jäi, võttis teine 1/17. Ta jättis riigikassasse 192. Tahame teada, kui palju oli riigikassas algselt
Akmim papüürus (VI c.)
3. Reisija! Siia matab tuha Diophantus. Ja numbrid võivad öelda, oh imet, kui pikk oli tema eluiga.
Tema kuues osa oli imeline lapsepõlv.
Möödus kaheteistkümnes osa teisest elust – siis oli lõug kohevaga kaetud.
Seitsmes lastetu abielu oli Diophantosel.
Viis aastat on möödunud; teda õnnistati kauni esmasündinu poja sünniga.
Kellele saatus kinkis isaga võrreldes vaid poole ilusast ja helgest elust maa peal.
Ja sügavas kurbuses võttis maise saatuse vanamees lõpuga vastu, olles poja kaotamisest neli aastat üle elanud.
Ütle mulle, mitu eluaastat võttis Diophantos surma vastu?
4. Keegi suremas pärandas: “Kui mu naisel on poeg, siis jäägu talle 2/3 pärandvarast, ülejäänud naisele. Kui sünnib tütar, on ta 1/3 ja naine 2/3. Sündisid kaksikud – poeg ja tütar. Kuidas pärandvara jagada?
Vana-Rooma ülesanne (II sajand)
Leidke kolm arvu nii, et suurim ületaks keskmist väikseima antud murdosa võrra, nii et keskmine ületaks väikseimat suurima murdosa võrra ja et väikseim ületaks 10 keskmise antud murdosa võrra.
Aleksandria Diophantose traktaat "Aritmeetika" (II-III sajand pKr)
5. Metspart lendab Lõunamerest Põhjamerre 7 päevaks. Metshani lendab põhjakaevandusest lõunamerre 9 päevaks. Nüüd lendavad part ja hani korraga välja. Mitme päeva pärast nad kohtuvad?
Hiina (2. sajand pKr)
6. “Üks kaupmees käis läbi 3 linna ja nad kogusid temalt tollimakse esimeses linnas poole ja kolmandiku vara eest ning teises linnas poole ja kolmandiku ülejäänud vara eest ning kolmandas linnas pool ja kolmandik ülejäänud varast. Ja kui ta koju jõudis, jäi tal 11 raha alles. Uurige, kui palju raha kaupmehel alguses oli.
Anani Shirakatsi. Kogumik "Küsimused ja vastused" (VIIsajandil pKr).
Seal on kadamba lill,
Ühe kroonlehe jaoks
Viiendik mesilastest on langenud.
Kasvab kohe selle kõrval
Kõik õitses Simengda,
Ja sellele mahtus kolmas osa.
Leiad nende erinevuse
Voldi see kolm korda kokku
Ja pange need mesilased kutai peale.
Ainult kahte ei leitud.
Sinu koht pole kuskil
Kõik lendasid edasi-tagasi ja igal pool
Nautis lillede lõhna.
Helista mulle kohe
Loen mõtetes
Mitu mesilast kokku on?
Vana-India ülesanne (XI sajand).
8. "Leidke arv, teades, et kui lahutate sellest kolmandiku ja veerandi, saate 10."
Muhammad ibn Musa al Khorezmi "Aritmeetika" (IX sajand)
9. Üks naine läks aeda õunu korjama. Aiast lahkumiseks pidi ta läbima nelja ukse, millest igaühel oli valvur. Naine andis pooled korjatud õuntest esimese ukse juures valvurile. Jõudnud teise valvuri juurde, andis naine talle poole ülejäänutest. Ta tegi sama ka kolmanda valvuriga ja kui ta jagas õunu neljanda valvuriga, jäi tal alles 10 õuna. Mitu õuna ta aias korjas?
"1001 ööd"
10. Ainult “see” ja “see” ning pool “sellest” ja “sellest” – kui palju on see protsent kolmveerandist “sellest” ja “sellest”.
Vana-Venemaa iidne käsikiri (X-XI sajand)
11. Kolm kasakat tulid karjapoisi juurde hobuseid ostma.
"Hea küll, ma müün teile hobused," ütles karjapoiss, "ma müün esimesele poole karja ja veel pool hobust, teisele pooled ülejäänud hobused ja veel pool hobust teisele ja kolmas. saada ka pooled ülejäänud hobused poole hobusega.
Ma jätan endale ainult 5 hobust."
Kasakad olid üllatunud, kuidas karjapoiss hobused osadeks jagab. Kuid pärast mõningast mõtlemist nad rahunesid ja tehing läks läbi.
Mitu hobust müüs karjapoiss igale kasakale?
12. Keegi küsis õpetajalt: "Ütle mulle, mitu õpilast teil klassis on, sest ma tahan anda teile oma poja õpetama." Õpetaja vastas: "Kui tuleb rohkem õpilasi kui mul on ja poole vähem ja neljas ja teie poeg, siis on mul 100 õpilast." Küsimus on selles, mitu õpilast õpetajal oli?
L. F. Magnitski "Aritmeetika" (1703)
13. Rändur, jõudes teisele järele, küsis temalt: "Kas see on kaugel eesolevast külast?" Teine reisija vastas: "Kaugus külast, kust te lähete, on võrdne kolmandikuga külade vahelisest kogukaugusest. Ja kui kõnnid veel kaks miili, oled täpselt külade vahel. Mitu miili on jäänud esimese reisijani minna?
L. F. Magnitski "Aritmeetika" (1703)
14. Taluperenaine müüs turul mune. Esimene klient ostis temalt pooled munad ja teine pool muna, teine pool ülejäänud ja teine pool muna ning kolmas viimased 10 muna.
Mitu muna talunaine turule tõi?
L. F. Magnitski "Aritmeetika" (1703)
15. Mees ja naine võtsid samast laekast raha ja midagi ei jäänud järgi. Abikaasa võttis 7/10 kogu rahast ja naine 690 rubla. Kui palju kogu raha oli?
L.N. Tolstoi "Aritmeetika"
16. Üks kaheksandik arvust
Võttes lisate sellele mis tahes
Pool kolmesajast
Ja kaheksa ületab
Mitte vähe – viiskümmend
Kolmveerand. mul on hea meel,
Kui see, kes skoori teab
See ütleb mulle numbri.
Johann Hemeling, matemaatikaõpetaja (1800)
17. Kolm võitsid natuke raha. Esimese osa moodustas sellest summast 1/4, teise osa - 1/7 ja kolmanda osa - 17 floriini. Kui suured on kõik võidud?
Adam Rize (Saksamaa, 16. sajand) 18. Otsustades jagada kõik oma säästud võrdselt kõigi poegade vahel, tegi keegi testamendi. „Minu vanim poegadest peaks saama 1000 rubla ja kaheksandiku ülejäänud osast; järgmine - 2000 rubla ja kaheksandik uuest saldost; kolmas poeg - 3000 rubla ja kaheksandik järgmisest saldost jne. ” Määrake poegade arv ja pärandatud säästude suurus.
Leonhard Euler (1780)
19. Kolm inimest tahavad osta maja 24 000 liivri eest. Nad leppisid kokku, et esimene annab poole, teine kolmandiku ja kolmas ülejäänud. Kui palju raha annab kolmas?
Murrud "," Tavaline fraktsioonid". Mäng "Sellest, mida nad suudavad ... vaimseks loendamiseks". Ülesanded teemale " Tavaline fraktsioonid ja tegevus nende peal” 1. U... filosoof, kirjanik. B. Pascal oli erakordselt andekas ja mitmekülgne, tema elu oli...
Murrud peetakse tänapäevani üheks kõige raskemaks matemaatika osaks. Murdude ajaloos on rohkem kui üks aastatuhandet. Võimalus terviku osadeks jagada tekkis Vana-Egiptuse ja Babüloni territooriumil. Aastatega muutusid murdosadega tehtavad toimingud keerulisemaks, muutus nende salvestamise vorm. Igal neist oli selle matemaatikaharu "suhtes" oma omadused.
Mis on murdosa?
Kui tekkis vajadus jagada tervik ilma tarbetute pingutusteta osadeks, tekkisid murded. Murdude ajalugu on lahutamatult seotud utilitaarsete probleemide lahendamisega. Mõistel "fraktsioon" on araabia juured ja see pärineb sõnast, mis tähendab "murdma, jagama". Alates iidsetest aegadest on selles mõttes vähe muutunud. Tänapäevane definitsioon on järgmine: murd on ühiku osa või osade summa. Vastavalt sellele kujutavad näited murdosadega matemaatiliste toimingute järjestikust täitmist arvude murdosadega.
Tänapäeval on nende salvestamiseks kaks võimalust. tekkisid eri aegadel: esimesed on iidsemad.
Tuli iidsetest aegadest
Esimest korda hakkasid nad fraktsioonidega opereerima Egiptuse ja Babüloni territooriumil. Kahe osariigi matemaatikute lähenemises oli olulisi erinevusi. Algus oli aga seal-seal sama. Esimene murd oli pool või 1/2. Siis tuli veerand, kolmandik jne. Arheoloogiliste väljakaevamiste kohaselt on fraktsioonide tekkimise ajalugu umbes 5 tuhat aastat. Esmakordselt leitakse arvu murdosasid Egiptuse papüürustest ja Babüloonia savitahvlitest.
Iidne Egiptus
Tavaliste murdude tüübid hõlmavad tänapäeval niinimetatud egiptuse murde. Need on mitme vormi 1/n liikme summa. Lugeja on alati üks ja nimetaja on naturaalarv. Sellised fraktsioonid ilmusid Vana-Egiptuses, ükskõik kui raske seda on arvata. Kõikide aktsiate arvutamisel üritati need selliste summadena (näiteks 1/2 + 1/4 + 1/8) alla kirjutada. Ainult murdudel 2/3 ja 3/4 olid eraldi tähised, ülejäänud jagunesid terminiteks. Seal olid spetsiaalsed tabelid, kus arvu murded esitati summana.
Vanim teadaolev viide sellisele süsteemile on leitud Rhinda matemaatilisest papüürusest, mis pärineb teise aastatuhande algusest eKr. See sisaldab murdude ja matemaatikaülesannete tabelit koos lahenduste ja vastustega, mis on esitatud murdude summadena. Egiptlased teadsid, kuidas arvu murde liita, jagada ja korrutada. Murrud Niiluse orus kirjutati hieroglüüfide abil.
Muistsele Egiptusele iseloomulikku arvu murdosa esitamist terminite summana kujul 1/n kasutasid matemaatikud mitte ainult selles riigis. Kuni keskajani kasutati Kreekas ja teistes osariikides Egiptuse fraktsioone.
Matemaatika areng Babülonis
Matemaatika nägi Babüloonia kuningriigis välja teistsugune. Murdude tekkelugu on siin otseselt seotud numbrisüsteemi tunnustega, mille muistne riik pärandas oma eelkäijalt, Sumeri-Akadi tsivilisatsioonilt. Arvutustehnika oli Babülonis mugavam ja täiuslikum kui Egiptuses. Matemaatika lahendas siin riigis palju laiemaid probleeme.
Babüloonlaste saavutusi võib tänapäeval hinnata säilinud kiilkirjaga täidetud savitahvlite järgi. Materjali omaduste tõttu on neid meieni jõudnud palju. Mõnede arvates avastati Babülonis enne Pythagorast tuntud teoreem, mis kahtlemata annab tunnistust teaduse arengust selles iidses riigis.
Murrud: murdude ajalugu Babülonis
Numbrisüsteem Babülonis oli seksagesiaalne. Iga uus kategooria erines eelmisest 60 võrra. Selline süsteem on tänapäeva maailmas säilinud aja ja nurkade näitamiseks. Murrud olid samuti seksagesimaalsed. Salvestamiseks kasutati spetsiaalseid ikoone. Nagu Egiptuses, sisaldasid murdnäidised 1/2, 1/3 ja 2/3 jaoks eraldi sümboleid.
Babüloonia süsteem ei kadunud koos riigiga. 60. süsteemis kirjutatud murde kasutasid iidsed ja araabia astronoomid ja matemaatikud.
Vana-Kreeka
Vana-Kreekas tavaliste murdude ajalugu eriti ei rikastatud. Hellase elanikud uskusid, et matemaatika peaks toimima ainult täisarvudega. Seetõttu murdosadega väljendeid Vana-Kreeka traktaatide lehtedel praktiliselt ei esinenud. Teatava panuse sellesse matemaatika harusse andsid aga pütagoorlased. Nad mõistsid murde suhet või proportsioone ning pidasid ka ühikut jagamatuks. Pythagoras ja tema õpilased koostasid üldise murdude teooria, õppisid sooritama kõiki nelja aritmeetilisi tehteid, samuti võrdlema murde, taandades need ühisele nimetajale.
Püha Rooma impeerium
Rooma murdude süsteemi seostati kaalumõõduga, mida kutsuti "perse". See jagunes 12 aktsiaks. 1/12 assat nimetati untsiks. Murdnimesid oli 18. Siin on mõned neist:
semis - pool assast;
sextante — kuues assa;
poolunts - pool untsi või 1/24 perset.
Sellise süsteemi ebamugavus seisnes selles, et arvu ei olnud võimalik esitada murdena, mille nimetaja on 10 või 100. Rooma matemaatikud said raskusest üle protsentide kasutamisega.
Harilike murdude kirjutamine
Antiikajal kirjutati murde juba tuttaval viisil: üks arv teise kohal. Siiski oli üks oluline erinevus. Lugeja oli nimetajast allpool. Esimest korda hakati murde sel viisil kirjutama Vana-Indias. Araablased hakkasid meie jaoks kasutama kaasaegset viisi. Kuid ükski neist rahvastest ei kasutanud lugeja ja nimetaja eraldamiseks horisontaalset joont. See ilmub esmakordselt Pisa Leonardo, paremini tuntud kui Fibonacci, kirjutistes 1202. aastal.
Hiina
Kui tavaliste murdude tekkimise ajalugu algas Egiptuses, siis kümnendkohad ilmusid esmakordselt Hiinas. Taevaimpeeriumis hakati neid kasutama umbes 3. sajandist eKr. Kümnendmurdude ajalugu sai alguse Hiina matemaatikust Liu Huist, kes tegi ettepaneku neid ruutjuurte eraldamisel kasutada.
3. sajandil pKr hakati Hiinas kaalu ja mahu arvutamiseks kasutama kümnendmurde. Tasapisi hakkasid nad üha sügavamale matemaatikasse tungima. Euroopas hakati aga kümnendkohti kasutama palju hiljem.
Al-Kashi Samarkandist
Olenemata Hiina eelkäijatest avastas kümnendmurrud iidse Samarkandi linna astronoom al-Kashi. Ta elas ja töötas 15. sajandil. Teadlane kirjeldas oma teooriat traktaadis "Aritmeetika võti", mis avaldati 1427. aastal. Al-Kashi tegi ettepaneku kasutada murdude jaoks uut tähistusvormi. Nii täis- kui ka murdosa kirjutati nüüd ühele reale. Samarkandi astronoom ei kasutanud nende eraldamiseks koma. Ta kirjutas täisarvu ja murdosa erinevates värvides, kasutades musta ja punast tinti. Mõnikord kasutas al-Kashi nende eraldamiseks ka vertikaalset joont.
Euroopas kümnendkohad
Uut tüüpi murrud hakkasid Euroopa matemaatikute töödesse ilmuma alates 13. sajandist. Tuleb märkida, et nad ei tundnud al-Kashi teoseid ega ka hiinlaste leiutist. Jordan Nemorariuse kirjutistes ilmusid kümnendmurrud. Siis kasutati neid juba 16. sajandil.Prantsuse teadlane kirjutas matemaatilise kaanoni, mis sisaldas trigonomeetrilisi tabeleid. Neis kasutas Viet kümnendmurde. Täisarvu ja murdosa eraldamiseks kasutas teadlane vertikaalset joont, aga ka erinevat kirjasuurust.
Need olid aga vaid teadusliku kasutuse erijuhud. Igapäevaprobleemide lahendamiseks hakati Euroopas kümnendmurde kasutama mõnevõrra hiljem. See juhtus tänu Hollandi teadlasele Simon Stevinile 16. sajandi lõpus. Ta avaldas 1585. aastal matemaatilise töö "Kümnes". Selles kirjeldas teadlane kümnendmurdude kasutamise teooriat aritmeetikas, rahasüsteemis ning mõõtude ja kaalude määramisel.
Punkt, punkt, koma
Stevin ei kasutanud ka koma. Ta eraldas murdosa kaks osa, kasutades ringikujulist nulli.
Esimest korda eraldas koma kaks kümnendmurru osa alles 1592. aastal. Inglismaal kasutati aga hoopis punkti. Ameerika Ühendriikides kirjutatakse kümnendmurrud endiselt sellisel viisil.
Üheks algatajaks mõlema kirjavahemärgi kasutamisel täis- ja murdosade eraldamiseks oli Šoti matemaatik John Napier. Oma ettepaneku tegi ta 1616.–1617. Koma kasutas ka üks saksa teadlane
Murrud Venemaal
Venemaa pinnal oli esimene matemaatik, kes visandas terviku osadeks jagamise Novgorodi munk Kirik. Aastal 1136 kirjutas ta teose, milles kirjeldas "aastate arvutamise" meetodit. Kirik tegeles kronoloogia ja kalendri küsimustega. Oma töös tõi ta välja ka tunni jagamise osadeks: viiendikuteks, kahekümneviiendikuteks jne.
Terviku osadeks jagamist kasutati maksusumma arvutamisel XV-XVII sajandil. Kasutati liitmise, lahutamise, jagamise ja korrutamise tehteid murdosadega.
Sõna "fraktsioon" ilmus Venemaal VIII sajandil. See pärineb tegusõnast "purustama, osadeks jagama". Meie esivanemad kasutasid murdude nimetamiseks spetsiaalseid sõnu. Näiteks 1/2 määrati pooleks või pooleks, 1/4 - neli, 1/8 - pool tundi, 1/16 - pool tundi ja nii edasi.
Täielik murdude teooria, mis ei erine palju tänapäevasest, esitati esimeses aritmeetikaõpikus, mille kirjutas 1701. aastal Leonti Filippovitš Magnitski. "Aritmeetika" koosnes mitmest osast. Murdudest räägib autor üksikasjalikult jaotises “Katkijoonte arvust või murdudega”. Magnitski annab tehteid "katkiste" numbritega, nende erinevad tähised.
Tänapäeval on murrud endiselt matemaatika kõige raskemate osade hulgas. Ka murdude ajalugu polnud lihtne. Erinevad rahvad, mõnikord üksteisest sõltumatult ja mõnikord oma eelkäijate kogemusi laenates, jõudsid vajaduseni tutvustada, meisterdada ja kasutada arvu murde. Murdude õpetus on alati välja kasvanud praktilistest tähelepanekutest ja tänu pakiliste probleemidele. Oli vaja leiba jagada, võrdsed maatükid maha märkida, makse arvutada, aega mõõta jne. Murdude ja nendega tehtavate matemaatiliste toimingute kasutamise tunnused sõltusid osariigi arvusüsteemist ja matemaatika üldisest arengutasemest. Ühel või teisel viisil, olles ületanud rohkem kui tuhat aastat, on arvude murdudele pühendatud algebra osa moodustunud, arenenud ja seda kasutatakse tänapäeval edukalt mitmesuguste praktiliste ja teoreetiliste vajaduste jaoks.
Murdude tekkelugu
Sissejuhatus
Vajadus murdarvude järele tekkis inimesel väga varases arengujärgus. Juba mitmest tapetud loomast koosnev saakloomade jagamine jahil osalejate vahel, kui loomade arv ei osutus jahimeeste arvu mitmekordseks, võis ürginimese viia murdarvu mõisteni.
Lisaks esemete loendamise vajadusele on inimestel iidsetest aegadest vajadus mõõta pikkust, pindala, mahtu, aega ja muid suurusi. Mõõtmiste tulemust ei ole alati võimalik väljendada naturaalarvuga ning arvesse tuleb võtta ka kasutatud mõõdiku osi. Ajalooliselt tekkisid fraktsioonid mõõtmisprotsessis.
Vajadus täpsemate mõõtmiste järele tõi kaasa selle, et esialgseid mõõtühikuid hakati jagama 2, 3 või enamaks osaks. Killustamise tulemusel saadud väiksemale mõõtühikule anti individuaalne nimi ja selle väiksema ühikuga mõõdeti juba väärtusi.
Murrud Vana-Roomas
Roomlaste seas oli peamine massi mõõtühik, samuti rahaühik oli "perse". Perse jagati 12 võrdseks osaks - untsiks. Nendest liideti kõik murrud nimetajaga 12 ehk 1/12, 2/12, 3/12 ... Aja jooksul hakati igasuguste koguste mõõtmiseks kasutama untse.
Nii on roomlane kaksteistkümnendmurrud, see tähendab murde, mille nimetaja on alati arv 12 . 1/12 asemel ütlesid roomlased "üks unts", 5/12 - "viis untsi" jne. Kolm untsi nimetati veerandiks, neli untsi kolmandikuks, kuus untsi pooleks.
Kasutusel oli ainult 18 erinevat fraktsiooni:
SIMIS - pool ässa;
SEKSTANCE - selle kuues aktsia;
SESSION - kaheksas;
TRIENCE – kolmandik ässast;
BES - kaks kolmandikku;
unts - perse kaheteistkümnendik;
SEMI-UNCE - pool untsi.
Murrud Vana-Egiptuses
Egiptlased nimetasid sadu sajandeid murde "katkenenud arvudeks" ja esimene murd, mida nad kohtasid, oli 1/2. Sellele järgnesid 1/4, 1/8, 1/16, ..., siis 1/3, 1/6, ..., s.o. lihtsamaid murde nimetatakse ühikuks või põhimurrud. Nende lugeja on alati üks. Alles palju hiljem hakkasid kreeklaste, seejärel indiaanlaste ja teiste rahvaste seas kasutusele võtma üldkuju murded, mida nimetatakse harilikeks murrudeks, milles lugejaks ja nimetajaks võivad olla mis tahes naturaalarvud.
Vana-Egiptuses saavutas arhitektuur kõrge arengutaseme. Suurejooneliste püramiidide ja templite ehitamiseks, kujundite pikkuste, pindalade ja mahtude arvutamiseks oli vaja tunda aritmeetikat.
Papüüruste dešifreeritud teabest said teadlased teada, et egiptlastel oli 4000 aastat tagasi kümnendarvu (kuid mitte positsiooniline) arvusüsteem, nad suutsid lahendada palju ehituse, kaubanduse ja sõjaliste küsimustega seotud probleeme.
Üks varasemaid teadaolevaid viiteid Egiptuse murdudele on matemaatiline papüürus Rhind. Kolm vanemat teksti, mis mainivad Egiptuse murde, on Egiptuse matemaatiline nahkrull, Moskva matemaatiline papüürus ja Akhmimi puidust tahvel. Rhinda papüürus sisaldab egiptuse murdude tabelit ratsionaalsete arvude jaoks kujul 2/ n, samuti 84 matemaatilist ülesannet, nende lahendusi ja vastuseid, mis on kirjutatud Egiptuse murdude kujul.
Egiptlased panid hieroglüüfi ( ep, "[üks]" või re, suu) numbri kohal, et tähistada tavalistes tähistes ühikulist murdu, ja pühades tekstides kasutasid nad rida. Näiteks:
Neil olid ka erisümbolid murdude 1/2, 2/3 ja 3/4 jaoks, mida sai kasutada ka teiste murdude (suuremad kui 1/2) kirjutamiseks.
Ülejäänud murrud kirjutasid nad aktsiate summana. Nad kirjutasid murdosa kui 
, kuid "+" märki ei näidatud. Ja summa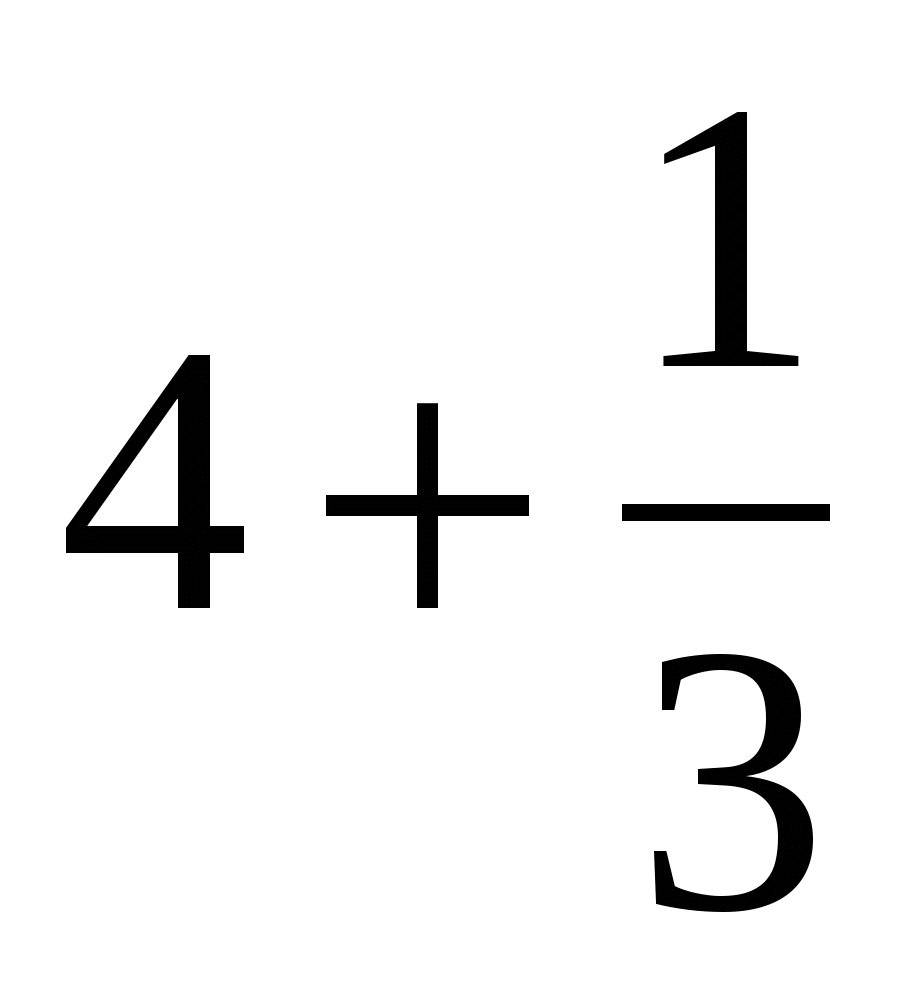 
vormis registreeritud 
. Seetõttu on selline segaarvude rekord (ilma "+" märgita) säilinud sellest ajast peale.
Babüloonia seksagesimaalsed murded
Vana-Babüloni elanikud, umbes kolm tuhat aastat eKr, lõid meie meetrilisega sarnase mõõtsüsteemi, ainult et see ei põhine mitte arvul 10, vaid arvul 60, milles väiksem mõõtühik oli 
osa kõrgemast üksusest. Seda süsteemi kasutasid täielikult babüloonlased aja ja nurkade mõõtmiseks ning me pärisime neilt tundide ja kraadide jagamise 60 minutiks ja minutite 60 sekundiks.
Teadlased selgitavad seksagesimaalarvusüsteemi ilmumist babüloonlaste seas erinevalt. Tõenäoliselt võeti siin arvesse baasi 60, mis on 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 ja 60 kordne, mis lihtsustab oluliselt kõikvõimalikke arvutusi.
Kuuekümnendad olid babüloonlaste elus tavalised. Sellepärast nad kasutasid seksagendiaalne murrud, mille nimetajaks on alati arv 60 või selle astmed: 60 2, 60 3 jne. Selles suhtes saab kuuekümnendmurdu võrrelda meie kümnendmurdudega.
Babüloonia matemaatika mõjutas Kreeka matemaatikat. Kaasaegses teaduses on aja ja nurkade mõõtmisel säilinud jäljed Babüloonia seksagesimaalarvusüsteemist. Tänaseni on säilinud jaotus tund 60 minutiks, minut 60 sekundiks, ring 360 kraadiks, kraad 60 minutiks, minut 60 sekundiks.
Babüloonlased andsid väärtusliku panuse astronoomia arengusse. Seksagesimaalseid murde kasutasid astronoomias kõigi rahvaste teadlased kuni 17. sajandini, nimetades neid astronoomiline fraktsioonid. Seevastu üldmurrud, mida me kasutame, nimetati tavaline.
Nummerdamine ja murded Vana-Kreekas
Kuna kreeklased tegelesid murdudega vaid juhuslikult, kasutasid nad erinevaid tähistusi. Vana-Kreeka matemaatikute seas kuulsaimad aritmeetikud Heron ja Diophantus kirjutasid murde tähestikulises vormis, nimetaja all oli lugeja. Kuid põhimõtteliselt eelistati kas ühe lugejaga murde või seksagesimaalseid murde.
Murdarvude kreeka tähistuse puudused, sealhulgas kuuekümnendmurdude kasutamine kümnendarvude süsteemis, ei olnud tingitud aluspõhimõtete puudustest. Kreeka arvusüsteemi puudujääkide arvele võib panna pigem nende kangekaelne ranguse soov, mis suurendas märgatavalt raskusi, mis on seotud võrreldamatute suuruste suhte analüüsiga. Kreeklased mõistsid sõna "arv" ühikute kogumina, nii et seda, mida me praegu peame üheks ratsionaalarvuks – murdarvuks, mõistsid kreeklased kahe täisarvu suhtena. See seletab, miks harilikud murrud olid kreeka aritmeetikas haruldased.
Murrud Venemaal
17. sajandi vene käsitsi kirjutatud aritmeetikas nimetati murde murdudeks, hiljem "katkearvudeks". Vanadest juhenditest leiame Venemaal järgmised murdude nimed:
1/2 - pool, pool
1/3 - kolmas
1/4 - neli
1/6 - pool kolmandikku
1/8 - poolteist tundi
1/12 - pool kolmandikku
1/16 - pool tundi
1/24 - pool kolmandikku (väike kolmandik)
1/32 - pool ja pool ja pool (väike veerand)
1/5 - viis
1/7 - nädal
1/10 - kümnis
Slaavi numeratsiooni kasutati Venemaal kuni 16. sajandini, seejärel hakkas järk-järgult riiki tungima kümnendkohanumbrite süsteem. Lõpuks asendas ta Peeter I all slaavi numeratsiooni.
Murrud teistes antiikseisundites
Hiina keeles “Matemaatika üheksas osas” toimuvad juba murdarvude vähendamised ja kõik toimingud murdudega.
India matemaatiku Brahmagupta juures leiame üsna arenenud murdude süsteemi. Tal on erinevad murded: nii põhi- kui ka tuletised suvalise lugejaga. Lugeja ja nimetaja kirjutatakse samamoodi nagu praegu, kuid ilma horisontaalse jooneta, vaid asetatakse lihtsalt üksteise kohale.
Araablased olid esimesed, kes eraldasid tulpa abil lugeja nimetajast.
Pisa Leonardo kirjutab juba murde üles, asetades segaarvu korral paremale täisarvu, kuid loeb seda nii nagu meil tavaliselt. Jordan Nemorarius (XIII sajand) jagab murde, jagades lugeja lugejaga ja nimetaja nimetajaga, võrdledes jagamist korrutamisega. Selleks peate täiendama esimese murru tingimusi teguritega:
15.-16. sajandil omandab murdude õpetus meile juba tuttava vormi ja võtab kuju ligikaudu just nendes lõikudes, mida meie õpikutes leidub.
Tuleb märkida, et aritmeetika jagamine murdude järgi on pikka aega olnud üks keerulisemaid. Pole ime, et sakslased pidasid kinni ütlusest: "Murdudeks kukkuda", mis tähendas - minna lootusetusse olukorda. Usuti, et kes murdu ei tunne, ei oska ka aritmeetikat.
Kümnendkohad
Kümnendmurrud ilmusid araabia matemaatikute töödesse keskajal ja iseseisvalt Vana-Hiinas. Kuid isegi varem, iidses Babülonis, kasutati sama tüüpi fraktsioone, ainult seksagesimaalseid.
Hiljem avaldas teadlane Hartmann Beyer (1563-1625) essee “Decimal Logistics”, kus ta kirjutas: “... Märkasin, et tehnikud ja käsitöölised väljendavad suvalise pikkuse mõõtmisel seda väga harva ja ainult erandjuhtudel samanimelised täisarvud; tavaliselt peavad nad võtma kas väikseid meetmeid või kasutama murdosasid. Samamoodi mõõdavad astronoomid suurusi mitte ainult kraadides, vaid ka kraadide murdosades, s.t. minutid, sekundid jne. Nende jagamine 60 osaks ei ole nii mugav kui 10, 100 osaks jne jagamine, sest viimasel juhul on palju lihtsam liita, lahutada ja üldiselt aritmeetilisi tehteid sooritada; Mulle tundub, et kümnendkohad, kui need kuuekümnendsüsteemi asemel kasutusele võtta, oleksid kasulikud mitte ainult astronoomia, vaid ka kõikvõimalike arvutuste jaoks.
Tänapäeval kasutame kümnendkohti loomulikult ja vabalt. Kuid see, mis meile tundub loomulik, oli keskaja teadlastele tõeliseks komistuskiviks. Lääne-Euroopa 16. sajandil koos täisarvude laialt levinud kümnendmurruga kasutati arvutustes kõikjal kuuekümnendmurde, mis pärinevad babüloonlaste iidsetest traditsioonidest. Hollandi matemaatiku Simon Stevini helge mõistus võttis nii täis- kui ka murdarvude rekordi koondamiseks ühte süsteemi. Ilmselt andsid kümnendmurdude loomise tõuke tema koostatud liitintressi tabelid. 1585. aastal avaldas ta raamatu "Kümnis", milles selgitas kümnendmurde.
17. sajandi algusest algab kümnendmurdude intensiivne tungimine teadusesse ja praktikasse. Inglismaal võeti täpp kasutusele märgina, mis eraldab täisarvu osa murdosast. Koma, nagu ka punkt, pakkus eraldajaks 1617. aastal matemaatik Napier.
Tööstuse ja kaubanduse, teaduse ja tehnika areng nõudis järjest tülikamaid arvutusi, mida oli kümnendmurdude abil lihtsam teostada. Kümnendmurrud võeti laialdaselt kasutusele 19. sajandil pärast nendega tihedalt seotud mõõtude ja kaalude meetrilise süsteemi kasutuselevõttu. Näiteks meie riigis, põllumajanduses ja tööstuses, kasutatakse kümnendmurde ja nende konkreetset vormi - protsenti - palju sagedamini kui tavalisi murde.
Kirjandus:
M.Ya.Vygodsky "Aritmeetika ja algebra antiikmaailmas" (M. Nauka, 1967)
G.I. Glazer “Matemaatika ajalugu koolis” (M. Education, 1964)
I.Ya.Depman "Aritmeetika ajalugu" (M. Enlightenment, 1959)
1 slaid
2 slaidi
* * http://aida.ucoz.ru Horatius "Luuleteadusest" "Albini poeg! Ütle mulle, kui võtame viis untsi ja lahutame ühe, mis siis jääb? - "Ässa kolmas osa." "Imeline! Noh, te ei raiska oma vara! Ja kui lisada eelmisele viiele üks, siis kui suur on kokku? - "Pool." (Tõlkinud M. Dmitriev.) http://aida.ucoz.ru
3 slaidi
* http://aida.ucoz.ru * Noorel roomal oli õigus! Selle ülesande lahendamisel saime ka: 5/12-1/12=1/3; 5/12+1/12=1/2. http://aida.ucoz.ru
4 slaidi
* http://aida.ucoz.ru "Pedikalt" Sünonüümid: täpne, peen, ettevaatlik, täpne, kohusetundlik, ehted, täpne, pedantne, filigraanne, puudulik. Ja see kummaline sõna "skrupulus" pärineb roomakeelsest nimest 1/288 assa - "scrupulus". http://aida.ucoz.ru
5 slaidi
* http://aida.ucoz.ru * Kasutusel olid ka sellised nimed: "semis" - pool perset, "sextans" - selle kuues osa, "seven unts" - pool untsi, see tähendab 1/ 24 perse jne .d. Kokku kasutati 18 erinevat murdnimetust. Murdudega töötamiseks oli vaja meeles pidada liitmistabelit ja korrutustabelit. Seetõttu teadsid Rooma kaupmehed kindlalt, et trientsi (1/3 perse) ja sekstanide liitmisel saadakse poolik ja kui bes (2/3 perse) korrutatakse sescutioniga (2/3 untsi, st. 1/8 perset), saadakse unts. Töö hõlbustamiseks koostati spetsiaalsed tabelid, millest osa on meieni jõudnud. http://aida.ucoz.ru
6 slaidi
Pärast võitu otsustas Gaius Julius Caesar oma avangardi premeerida ja eraldas neile kõigepealt 24 untsi ja seejärel veel 36 untsi. Mitu ässa sai salk? Otsus: 24 untsi on 2 eesli ja 36 untsi on 3 eesli, üksus võttis vastu 3 + 2 = 5 eesli. Vastus: 5 perset. Miša Ivanovi probleem
7 slaidi
Angelina Glibina ülesanne Vana-Roomas autasustati auväärselt lahingus jõudu ja julgust üles näidanud sõdalasi. Mitu ässa kulus 6 sõdalase premeerimiseks, kui igaühele anti 2 ässa ja 6 untsi. Lahendus: korrutame 6 2 eesliga, saame 12 eesli - see on antud ainult 6 sõdalase kohta, siis korrutame 6 6-ga, saame 36 untsi ja ühes persis - 12 untsi, saame 3 eesli, lisame 3 kuni 12, saame 15 eeslit . Vastus: 15 perse.
